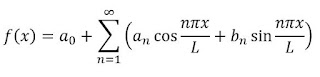The advantage with this approach is reduces the problem to an algebra problem. However, this may work only on limited classes of g(t).
We can write y(x) as,
Where,
Let's solve this given SODE,
We first solve for yh,
Since they are real roots, we have yh as,
For yp, we have to guess what it looks like based on g(x). The table below will help us to determine that.
Since g(x) = 3e^(5x), then our yp guess is,
We can plug yp guess to get our actual yp,
we now have y(x) and y'(x) as follows,
To get c1 and c2, we set x = 0 with the above equations,
Now, we have our actual solution,